Your last paragraph is so wrong except for the last sentence.Holy hell you are dense. The argument has always been the same as I thought people might gain some perspective after looking at the CDC data for kids/young adults. Obviously it required me to walk you all the way through the basic math.
The answer for your insanely dumb question can be found in the thread title: the leagues are starting to shut it down.
If the leagues are willing to accept the risks associated with CTE them they should be willing to risk Covid. If the players want to play, let them play. If they opt out they should be able to keep their scholarship.
-
Prime Time. Prime Time. Its a new era for Colorado football. Consider signing up for a club membership! For $20/year, you can get access to all the special features at Allbuffs, including club member only forums, dark mode, avatars and best of all no ads ! But seriously, please sign up so that we can pay the bills. No one earns money here, and we can use your $20 to keep this hellhole running. You can sign up for a club membership by navigating to your account in the upper right and clicking on "Account Upgrades". Make it happen!
You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
2020 CU football season POSTPONED until Nov 6th?
- Thread starter Jens1893
- Start date
class01
Well-Known Member
Do you mean the competition that is getting wrapped up in a stripped down form at a hub in Portugal to avoid unnecessary travel across a continent that has a fraction of the number of infections the US has?
Europe does not have the fraction of cases of the US. If you pool the data from the top 6 countries to get an equivalent population the death totals are the same (we would compare favorably if not for Cuomo). Trump is too stupid to explain it correctly, but our %positive is in line with the rest of the world and actually 4X better than France.
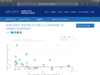
Europe does not have the fraction of cases of the US. If you pool the data from the top 6 countries to get an equivalent population the death totals are the same (we would compare favorably if not for Cuomo). Trump is too stupid to explain it correctly, but our %positive is in line with the rest of the world and actually 4X better than France.
This conveniently ignores the timing of virus deaths in Europe and NY. It's true that the fatality rate in some European countries is higher (presently) than the rate in the U.S.

It's also true that about 1,000 people died from COVID in the U.S. yesterday. While the UK, Spain, Italy, and France had 55, 0, 13, and 0 deaths yesterday.
It's true that somebody is too stupid to correctly explain the difference between current infection/death rates in the U.S. and Europe.
You have to wonder when some of the MAC teams throw in the towel on football. Don’t get me wrong, they can field some decent teams, but they have pretty small cash flow from operations. Almost everything comes from institutional support and student fees.
I'm guessing that most of the MAC programs make a good deal of their revenue from all the games they play against Big 10 teams every year, so when the Big 10 said they were going conference-only that was a huge hit to alot of these programs. And then they ended up losing a number of other games against P5 teams when the rest of the conferences went conference-only. It's not really surprising that they ended up cancelling given that most if not all of the MAC schools lost their biggest revenue game, and a few schools had 2 games against P5 teams.
The vast majority of them, yes. The select few that are really part of the minor league for professional sports, maybe, maybe not.And that's exactly what the athletes will do!
In my opinion, it is very important to transition to thinking about acceptable risk explicitly in regards to COVID-19; and the comparison to CTE is a reasonable and potentially useful comparative tool. I do take issue with your method, namely no citation of your numbers and no apparent consideration of the uncertainty of those estimates.There are 5M confirmed cases of SARS-CoV2 In the US. Let’s say the true # is 10X higher @ 50M out of a total US population of 328M which = 15% positive. There are a total of 12,659 CFB players and let’s assume they also get infected at the same rate despite some of the mitigation efforts mentioned (15% = 1928). The fatality rate/infection for their age group is 0.001% which means 0.02 players are likely at risk at most. The fatality rate is likely much lower for elite athletes vs. the general pop with whatever percentage of co-morbidities (obesity, cancer, diabetes etc).
I’m not saying the 2020 CFB season is necessarily worth risking a ~0.0001-0.0002% chance of death or any of the unknown long-term consequences, but I guarantee that >1 player will get CTE and/or long-term disabilities associated with traumatic brain injury. What is the difference between CTE and Covid liability for universities? If you can accept the risk associated with CTE you shouldn’t be worried about Covid. If you are super conservative and say 10% of CFB players will suffer significant CTE then Covid is somewhere around 60,000-fold less dangerous.
Stadiums filled with fans are not a good idea, but the kids should be able to play if they want to. Champions league is going fine.
You've done a back of the envelope calculation with numerous assumptions and estimated parameters that provide zero context about any uncertainty about those assumptions and estimates.
Even if the inputs (lacking citations) are the appropriate estimates based on current available evidence, your conclusion ignores the underlying uncertainty. You could be talking about a most likely 1/50 chance that one player dies, while ignoring a very appreciable chance that tens or hundreds of players could die.
If I'm able to find time, I may work up a more data driven counter argument, for now I can provide one anecdote that should illustrate a glaring limitation of you estimates.
You work from a 15% prevalence rate, in the MLB we have 2 teams that have already experienced outbreaks among their 30 player rosters just two weeks into the season. The Cardinals, so far, have 9 players who tested positive (30% of the roster), and the Marlins had 18 players test positive (60%). There is clear evidence that at least in those cases, a group of young athletes sharing locker rooms, practicing and playing together, can experience an outbreak that is far more widespread than your stated estimate. This alone would multiply your estimate by at least a factor of 2 or 4; now imagine if we bump the extremely low stated fatality rate up to as still extremely low rate of 0.001%, in combination we're now multiplying your estimate by a factor of 20 or 40.
These are small adjustments to your assumptions and drastically change the outcome; any good model would include sensitivity analysis and a discussion of uncertainty of parameter estimates.
Shorter class01: I want fall football, and I'm going to make any argument I can to say why it should happen.
somebody
Well-Known Member
Lol, I assumed you referred to players' health choices, because it's pretty obvious COVID is additional risk to the leagues. Assuming they even do this calculation, having the CTE liability would make them more wary to take on new liability. That should be obvious, even to you.Holy hell you are dense. The argument has always been the same as I thought people might gain some perspective after looking at the CDC data for kids/young adults. Obviously it required me to walk you all the way through the basic math.
The answer for your insanely dumb question can be found in the thread title: the leagues are starting to shut it down.
If the leagues are willing to accept the risks associated with CTE them they should be willing to risk Covid. If the players want to play, let them play. If they opt out they should be able to keep their scholarship.
ahoelsken
Well-Known Member
You have to wonder when some of the MAC teams throw in the towel on football. Don’t get me wrong, they can field some decent teams, but they have pretty small cash flow from operations. Almost everything comes from institutional support and student fees.
They're not in as bad a shape as you think they are, but the paycheck games they get against the P5 are pivotal for them. Went through and looked at all their OOCs for 2021. Every MAC team plays at least one roadie at a power 5 school and 7 MAC teams are playing two. Take those away and add in no fans (in all likelihood) and that league being the first to say "We'll cancel the fall and try for the spring" is easy.
It was a joke played on the fact they will just go and study.The vast majority of them, yes. The select few that are really part of the minor league for professional sports, maybe, maybe not.
class01
Well-Known Member
This conveniently ignores the timing of virus deaths in Europe and NY. It's true that the fatality rate in some European countries is higher (presently) than the rate in the U.S.

It's also true that about 1,000 people died from COVID in the U.S. yesterday. While the UK, Spain, Italy, and France had 55, 0, 13, and 0 deaths yesterday.
It's true that somebody is too stupid to correctly explain the difference between current infection/death rates in the U.S. and Europe.
You are only proving my point that people such as yourself lack perspective. My point was that Europe basically has the same# of cases as we do. We did see a recent "spike" in cases/deaths (protests??). Rates are a function of time which you kind of acknowledged at the beginning of your post, but you revealed your lack of understanding by trying to use the single day data from yesterday (myopic). From the CDC:
They're not in as bad a shape as you think they are, but the paycheck games they get against the P5 are pivotal for them. Went through and looked at all their OOCs for 2021. Every MAC team plays at least one roadie at a power 5 school and 7 MAC teams are playing two. Take those away and add in no fans (in all likelihood) and that league being the first to say "We'll cancel the fall and try for the spring" is easy.
Exactly
Testing inadequacies and emerging cardio concerns (SI article) will draw the season to a close very soon, maybe even this week.
Expect the Pac-12 and Big 10 to announce by the end of the day Tuesday.
Please stop being a clown. Total number of historical cases is irrelevant when making decisions about how risky any particular activity is. What matters is current infection rate. And since the current infection rate in many parts of the U.S. is many times higher than the current rate in Europe and NYC, we will likely not have a fall CFB season. You can feel free to attribute this to some sort of heightened risk aversion. You'll be wrong, though. The blame lies with our failure to take the necessary steps to sufficiently reduce the spread of the virus.You are only proving my point that people such as yourself lack perspective. My point was that Europe basically has the same# of cases as we do. We did see a recent "spike" in cases/deaths (protests??). Rates are a function of time which you kind of acknowledged at the beginning of your post, but you revealed your lack of understanding by trying to use the single day data from yesterday (myopic). From the CDC:
View attachment 38638
White_Rabbit
Well-Known Member
what a sad state the country is in where staying on a campus and playing football is considered safer than going home.
between the howell op ed suggesting we are nearing the cancellation and now this ESPN rumor...

 www.espn.com
www.espn.com
have to figure it is pretty likely the p12 and b10 cancel, at least for the fall.
it is a bigger problem than sports. as soon as all those thousands of students head back to school via trains, planes, and automobiles, the mobility of infection will go through the roof. and, then, when they start getting the virus and schools are forced to close, the students are going to disperse to all over via trains, planes, and automobiles, taking the infection with them.
the responsible thing to do is start everywhere via remote learning at every level. and then see if we can get some containment. that can lead to how one has a sports calendar.
we haven't done enough to earn college sports in terms of containment, and the student-athletes playing the game are being asked to do too much for not nearly enough.
this isn't ok.

Sources: Power 5 talking about no fall football
Power 5 commissioners met to discuss canceling football and other fall sports, sources told ESPN.
have to figure it is pretty likely the p12 and b10 cancel, at least for the fall.
it is a bigger problem than sports. as soon as all those thousands of students head back to school via trains, planes, and automobiles, the mobility of infection will go through the roof. and, then, when they start getting the virus and schools are forced to close, the students are going to disperse to all over via trains, planes, and automobiles, taking the infection with them.
the responsible thing to do is start everywhere via remote learning at every level. and then see if we can get some containment. that can lead to how one has a sports calendar.
we haven't done enough to earn college sports in terms of containment, and the student-athletes playing the game are being asked to do too much for not nearly enough.
this isn't ok.
class01
Well-Known Member
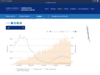
Please stop being a clown. Total number of historical cases is irrelevant when making decisions about how risky any particular activity is. What matters is current infection rate. And since the current infection rate in many parts of the U.S. is many times higher than the current rate in Europe and NYC, we will likely not have a fall CFB season. You can feel free to attribute this to some sort of heightened risk aversion. You'll be wrong, though. The blame lies with our failure to take the necessary steps to sufficiently reduce the spread of the virus.
Here is the current infection rate clown (updated today). Follow the blue line. The current rate seems to be trending the right direction. The setback in July seems to align with the protests and likely the wave as it passed through Mexico - but, I shouldn’t speculate to avoid offending anyone.
class01
Well-Known Member
Ah yes, the mention of protests. No agenda there.
Ignore the data. Bury your head in the sand. Trust the politicians because they will do the best thing for us and not them.
Ignore the data. Bury your head in the sand. Trust the politicians because they will do the best thing for us and not them.
Yikes.
somebody
Well-Known Member
Whereas your big idea is the leagues carry a lot of risk, so they should be willing to carry more risk. Does that really make sense to you?Ignore the data. Bury your head in the sand. Trust the politicians because they will do the best thing for us and not them.
I think B1G tomorrow. Their presidents meet tonight.Expect the Pac-12 and Big 10 to announce by the end of the day Tuesday.
P12 and b12 top dogs meet Tues. ACC Wed. SEC Thurs. Numerous G5 top exec meetings M, T W.
It’s over.
I get what Lawrence is saying, but at the same time, the argument he and others are making is that kids will only do the things necessary to keep themselves safe if the coaches and staff are forcing them to do it. The fly in that ointment is that we are already seeing examples where programs are not being forthright on that, so the argument is really a specious one, at best.
Whether you agree or disagree with Mr. Lawrence, you have to admit that’s a pretty reasonable argument to make.
